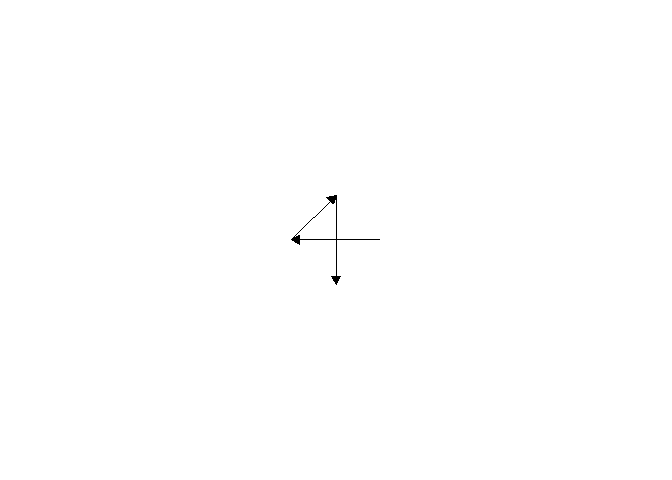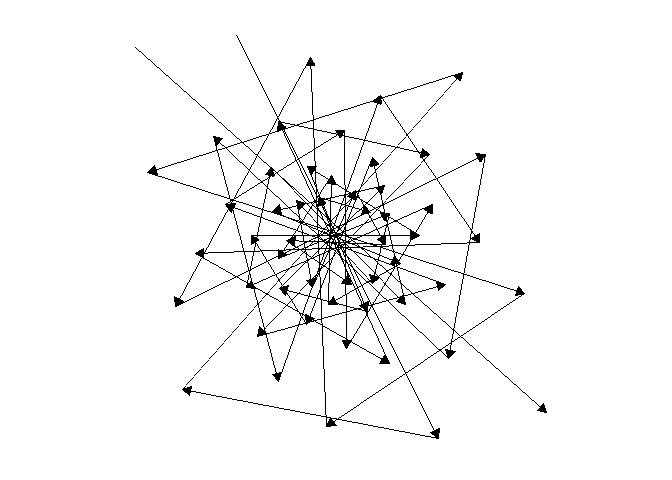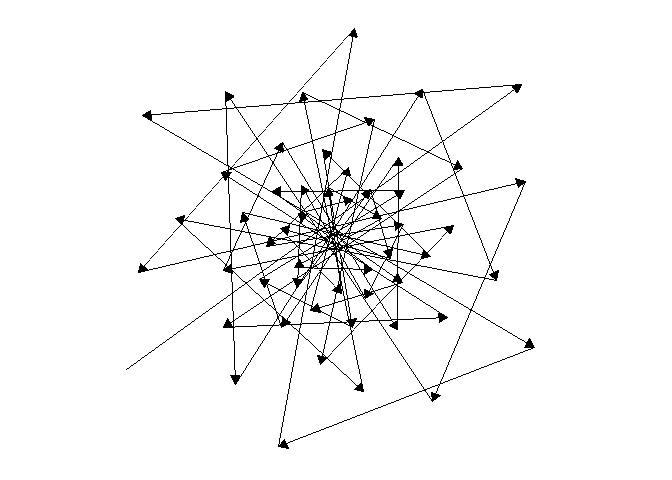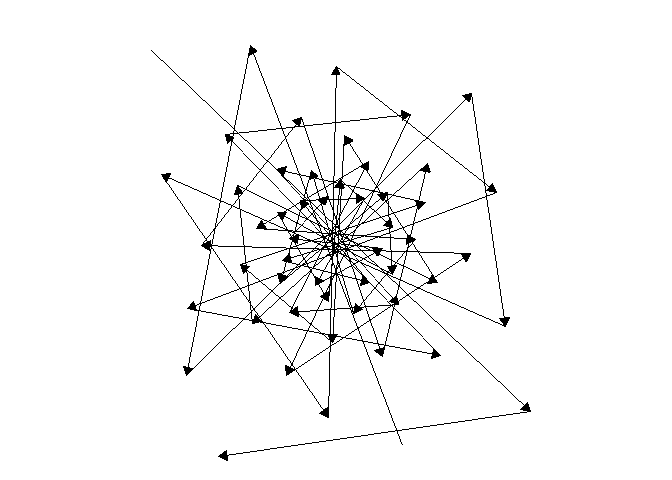
Plants and the Fibonacci series
This post started a few months ago when I saw a recent study in Science come up in my news feed. Scientists had examined a three-dimensional lycopod (club moss) fossil and determined that its leaves formed non-Fibonacci spirals, which is something not seen in most modern plants (Turner et al. 2023). But I was left wondering, what exactly is a Fibonacci spiral, and why do plants form that shape? Despite the fact that people have been studying the occurrence of Fibonacci patterns in nature for hundreds of years, I had trouble finding layperson-oriented materials on the internet to answer my questions. So I dived into the primary literature, braved a lot of jargon and equations, and got my answer. Apologies that a lot of my references for this post are behind a paywall!
Glossary
alternate: in botany, the case where a single leaf emerges at each height along a stem
apical: referring to the top or apex, like the top of a tree
axillary: near the axil, where the leaf connects to the stem
decussate: cross-shaped. In botany, an opposite arrangement of leaves where each pair is at a 90° angle from the last pair.
distichous: opposite or alternate leaf arrangement, where all leaves line up with each other in two columns 180° apart from each other
inflorescence: a group of flowers growing along a stem
meristem: the “stem cells” of a plant, at the tip of a shoot, branch, or root, that give rise to all other organs
opposite: in botany, the case where two leaves emerge at the same height on a stem, 180° apart from each other
parastichy: a spiral pattern of leaves or flowers originating from a single primordium
phyllotaxis: the arrangement of leaves and flowers around a stem
primordium (pl. primordia): a mound of cells on the side of a meristem that will become an organ such as a leaf, along with a new meristem
shoot apical meristem (SAM): the meristem at the top of the plant (e.g. the tip of a tree trunk) that gives rise to branches, leaves, and possibly flowers
whorled: in botany, two or more leaves coming out of a stem at the same height
The Fibonacci series is an endless sequence of numbers, where each number is the sum of the two numbers before it. 1, 1, 2, 3, 5, 8, 13, 21, 34, etc. As the series approaches infinity, the ratio between any number and the previous number in the sequence approaches \(\frac{1 + \sqrt{5}}{2}\), or about 1.62, also known as the golden ratio. On many plants, two successive leaves or flowers on a stem are pointed at a 137.5° angle from each other, which is known as the golden angle because (360°- 137.5°) / 137.5° = 1.62 (Douady and Couder 1996a; Shi and Vernoux 2019). So this angle between leaves is one way that the golden ratio, and by extension the Fibonacci series, is found in plant geometry. If you go for a walk and start looking at plants, you will not have to go far at all to find leaves or flowers pointing at the golden angle from each other along a stem.
I even saw this pattern in saw palmetto, although it would have been difficult to capture in a photograph.
When leaves or flowers are packed very tightly together and arranged with the golden angle, we see the Fibonacci series in a second way. Organs that are in contact with each other form sets of spirals, called “contact parastichies”, one set that goes clockwise, one that goes counter-clockwise, and perhaps a third that goes more vertically down the stem. And the respective numbers of parastichies in these sets are almost always adjacent numbers in the Fibonacci series (Douady and Couder 1996a; Newell and Shipman 2005).
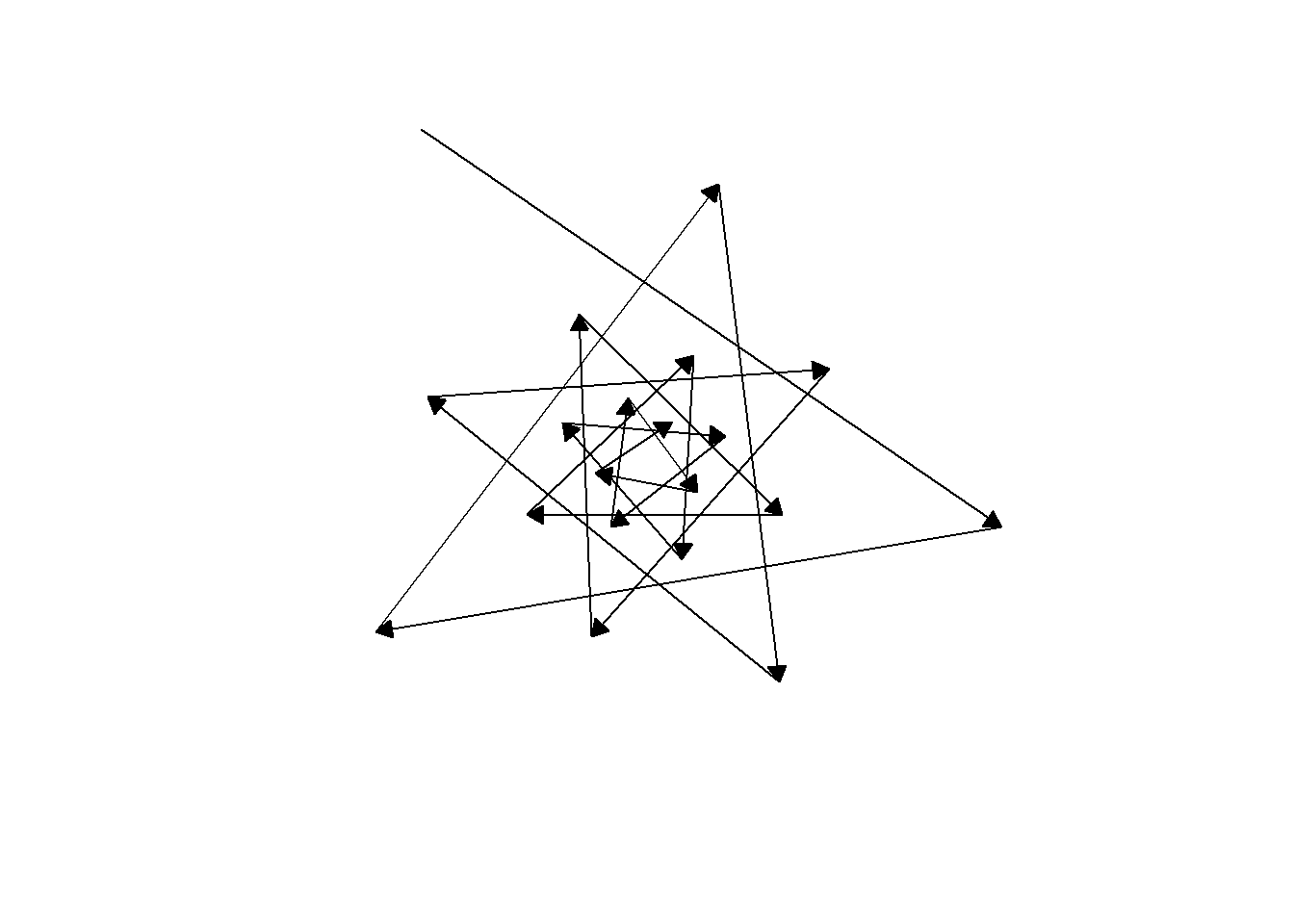
I have to admit I didn’t really have in my mind’s eye what shape I would make from tracing the order of leaf emergence on the succulent. Infinite pentagram (infinigram?)! Because the golden ratio is an irrational number, two points on the star will never perfectly line up and it will never close. Perhaps a symbol of the infinite facets to our inner and outer worlds. Of course, I love the symbolism of spirals as well and discussed that a bit in my post on magnolia.
I’ll leave it as an exercise for the reader to make a similar diagram using a photograph of a sunflower head. It is common to see 21, 34, 55, or even 89 parastichies (Swinton, Ochu, and The MSI Turing’s Sunflower Consortium 2016)!
Of course, not all plants form Fibonacci spirals. Here is an example of a pattern called “decussate”, in which pairs of opposite leaves emerge at 90° angles to each other.
There is also “distichous” where all leaves line up in two columns 180° apart.
Lastly, not pictured, leaves can be arranged in whorls, in which three or more leaves emerge at evenly-spaced angles at the same point on the stem.
If you want to see a video that shows these patterns in 3D and also makes the math really approachable, check out Doodling in math: Spirals, Fibonacci, and being a plant by Vi Hart.
Modelling the meristem
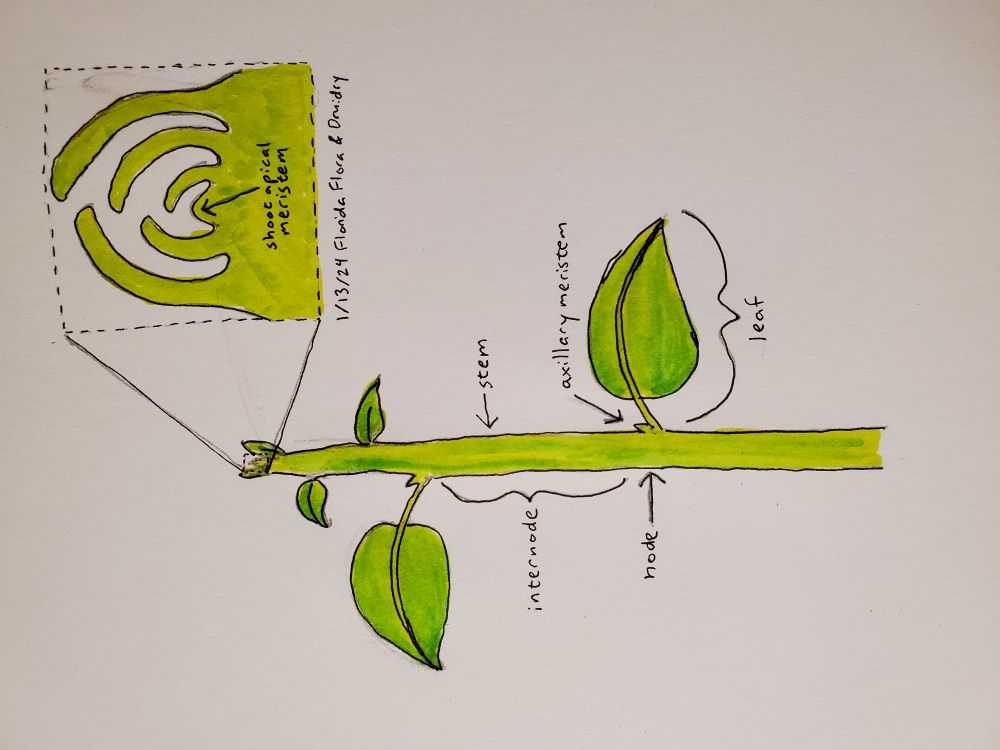
So where do these patterns come from? All leaves start their lives as leaf primordia at the very tip of a branch or shoot, in the meristem, a microscopic cluster of stem cells. The cells of the meristem are constantly dividing as the shoot grows, leaving behind stem and leaves as the meristem moves upward. The youngest leaves curl around the meristem to form a protective layer, visible as a bud on a plant. Figure 1 of Barton (2010) has a nice diagram of an Arabidopsis plant as well as some pictures of a meristem. The primary meristem at the top of a plant is usually called the shoot apical meristem. Just above the base of each leaf, there is also an axillary meristem. Most axillary meristems stay dormant, but some grow into branches, and if the shoot apical meristem is lost one of the axillary meristems will take over that role, its branch becoming the main trunk of the plant. A location along the stem that has a leaf and an axillary meristem is called a node, and the stem in between nodes is called internode.
Nodes and internodes in the garden
As a gardener or forager, it is really helpful to understand these patterns of plant development. If you go out and look at your plants every day you probably already have a sense of how they develop. If you are going to cut off part of a plant, or evaluate the viability of a plant that got munched by an herbivore last night, look at the remaining nodes and you’ll be able to visualize how the plant can grow new branches. While it’s good to leave an inch or so of internode above a node as a buffer against infection, be aware that the internode doesn’t have any potential to grow new leaves and branches.
Cauliflower
If you want to see a meristem with your own eyes, look no further than the produce section of the grocery store. Cauliflower is a meristem gone haywire. Instead of developing into flowers, the primordia just form new meristems, which in turn form new primordia which form new meristems. There are “fractal” varieties of cauliflower, but even on an ordinary variety you can see the fractal pattern, complete with Fibonacci numbers of contact parastichies, if you look closely. In normal plants there are genes that turn each other on and off like a set of switches to tell each primordium what it is going to become, for example a leaf or flower. In cauliflower, the switch to tell a primordium to become a flower flips back off due to a mutation, and the primordium then thinks it should be an inflorescence meristem (like the one that generated it), hence the fractal pattern. Researchers have fairly recently figured out the gene network that causes the flower to inflorescence transition in cauliflower (Azpeitia et al. 2021). Check out Figure 1 of their article if you want to see an illustration of cauliflower spirals.
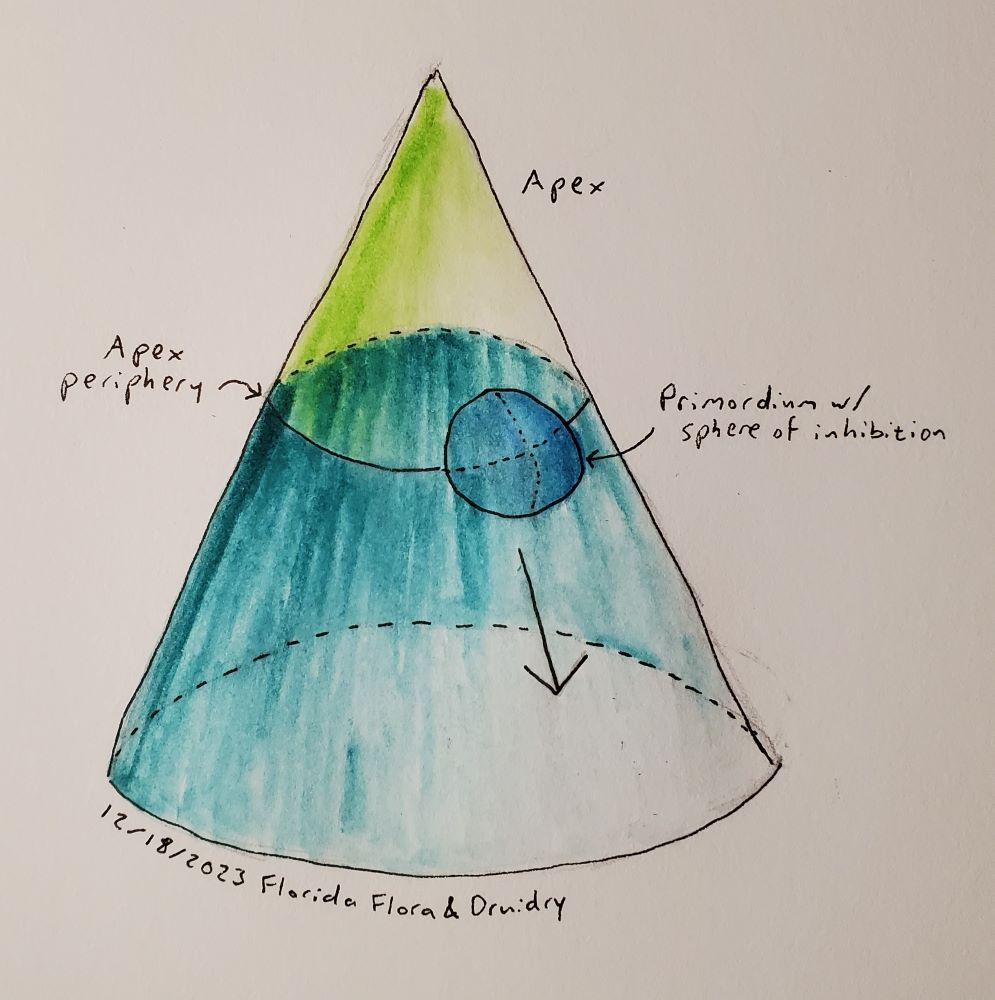
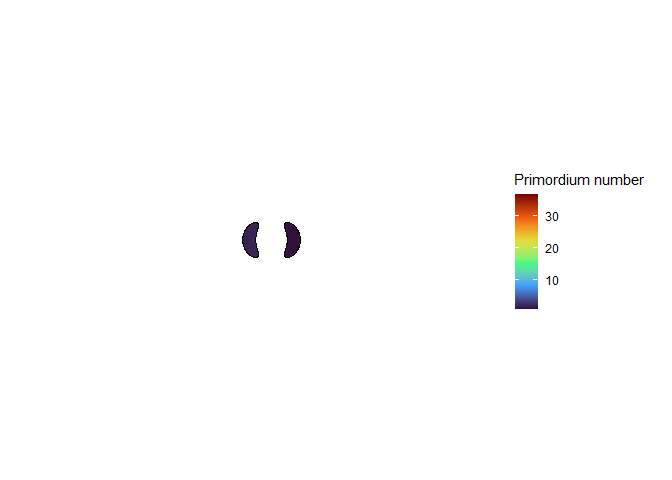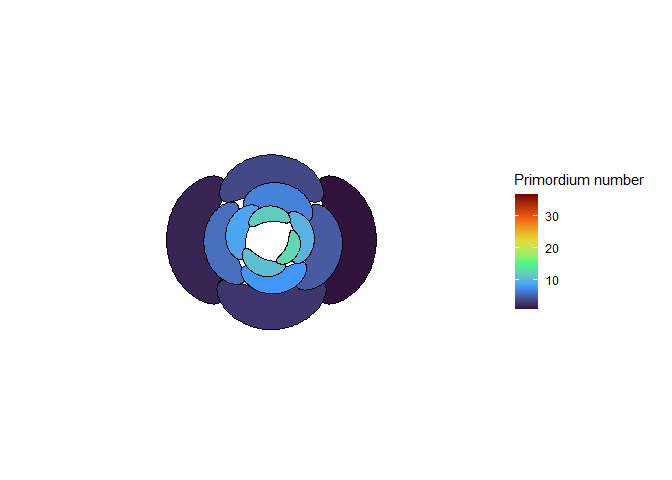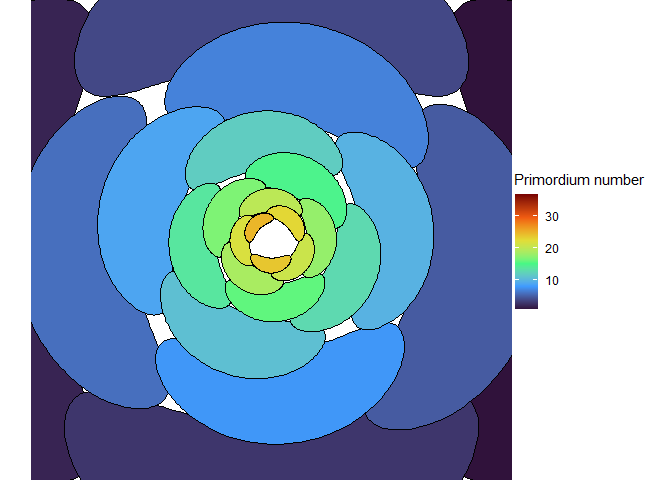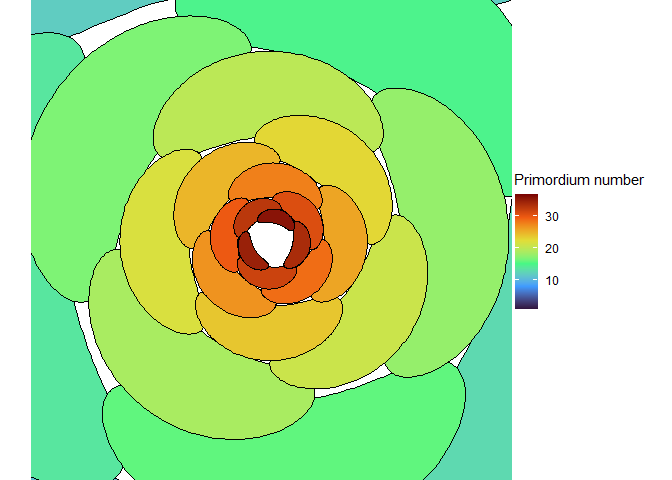
In a widely-cited, three-part article series, Douady and Couder described a model for how primordia arrange themselves on a meristem to create patterns of phyllotaxis, and they tested their model with drops of magnetic fluid as well as computer simulations (Douady and Couder 1996a, 1996b, 1996c). In their model, the meristem is a cone. The tip of that cone, called the apex, is made of stem cells. Under the apex is a circle going around the cone called the apex periphery, where all primordia start. As the plant grows, primordia move down from the apex periphery at an exponential rate, which is to say their rate of movement is proportional to how far away they are. Each primordium emits some sort of signal that prevents other primordia from forming within a certain distance, and the signal travels through the middle of the cone as well as along its surface. Although the primordia grow as they move down the cone, the diameter of this inhibitory sphere does not grow. New primordia form along the apex periphery at the point of minimum energy, i.e. the point furthest away from other primordia, as soon as there is such a point that is not within any sphere of inhibition.
By adjusting the following parameters, Douady and Couder were able to generate most patterns of phyllotaxis seen in nature:
The size of the inhibitory sphere, relative to the diameter of the apex periphery
The angle of the cone
Starting conditions being symmetrical or asymmetrical. To make asymmetrical starting conditions, you can put two primordia at some angle other than 180° to each other, at two different distances from the tip of the meristem.
The stiffness of repulsion, i.e. how quickly the signal inhibiting new primordia from forming drops off outside of the inhibitory sphere. This didn’t seem to have as much of an impact, so they picked one value and stuck with it for all of the results presented in their papers.
The famous statistician George Cox once said “All models are wrong, but some are useful.” This essentially means that no statistical or scientific model can possibly take all factors into account, but if the model can be used to predict real-world events then it is useful. Meristems only consist of a lumpy handful of cells, so it doesn’t seem possible that they would be perfectly cone-shaped, or that a signal to inhibit the formation of primordia would diffuse totally evenly, or that primordia would move away from the apex at a smoothly increasing rate. So, the model of Douady and Couder can’t possibly be 100% accurate, but it is useful for describing the diversity of patterns of phyllotaxis seen in real world plants. The same can be said of spiritual beliefs, can’t it? For example, we know that the universe is not literally made of the elements earth, air, fire, and water, but druids and many others find it useful to frame their experiences around these elements and what they symbolize.
I wanted to see Douady and Couder’s model in action, so I wrote some custom functions in the R programming language to follow their equations, and used gganimate to make animations of the simulated meristems. (Douady and Couder didn’t publish their computer code because that wasn’t yet common practice in the 90’s, and besides that it was written in Think Pascal, which was discontinued one year after the papers were published.) It took a bit of work, but I was very excited to see something that looked like a plant.
Still image
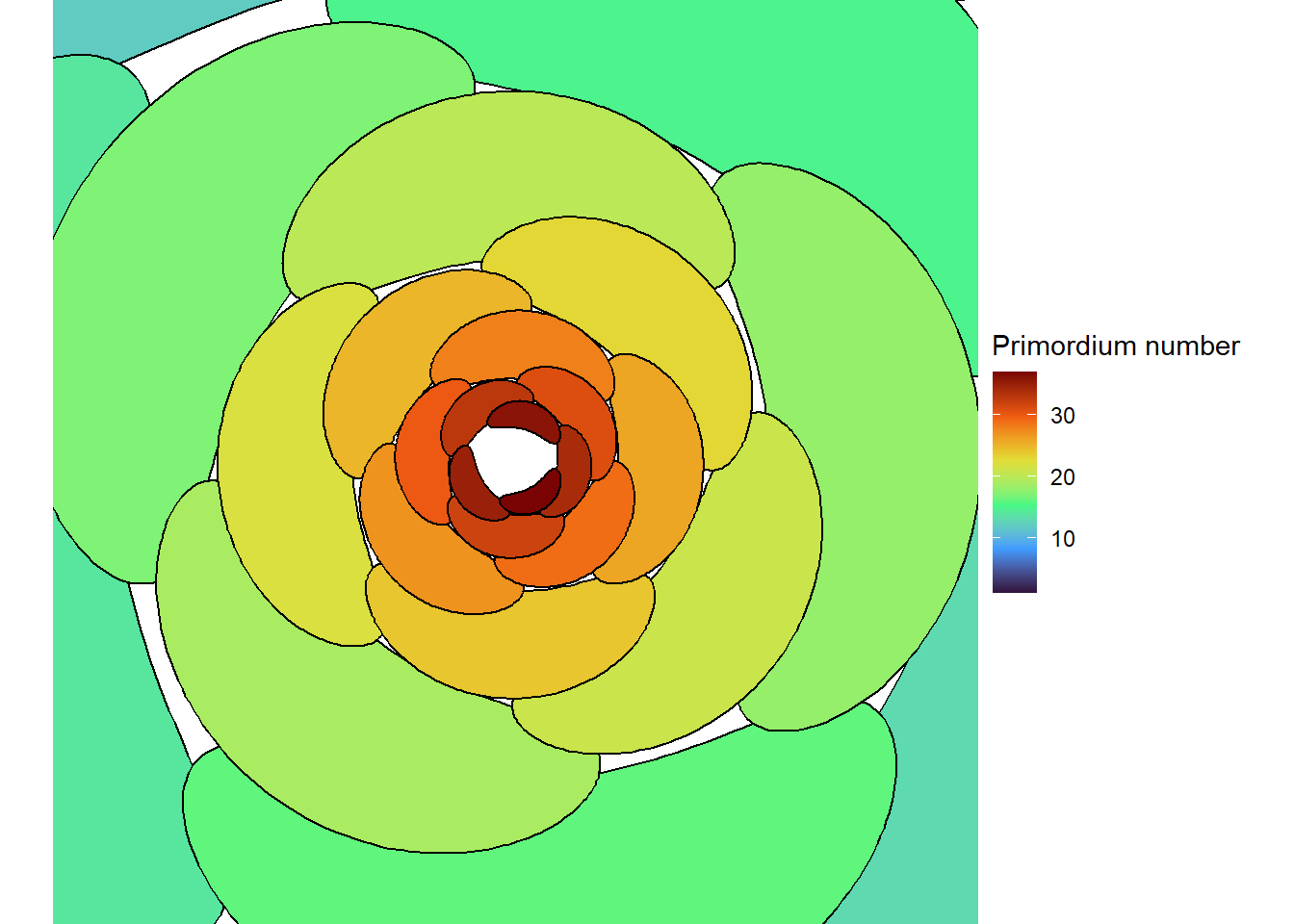
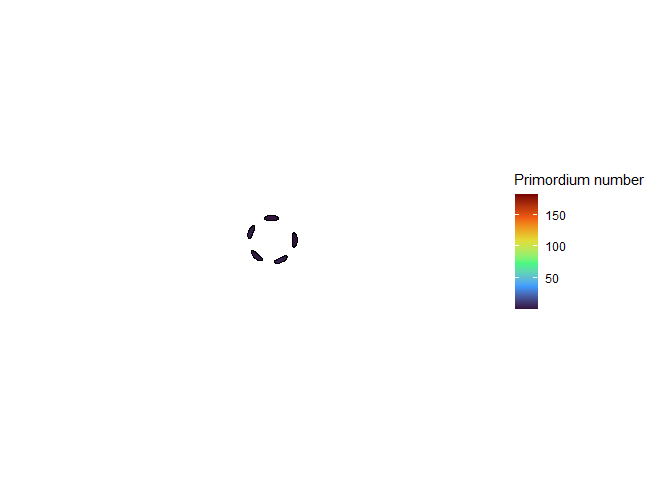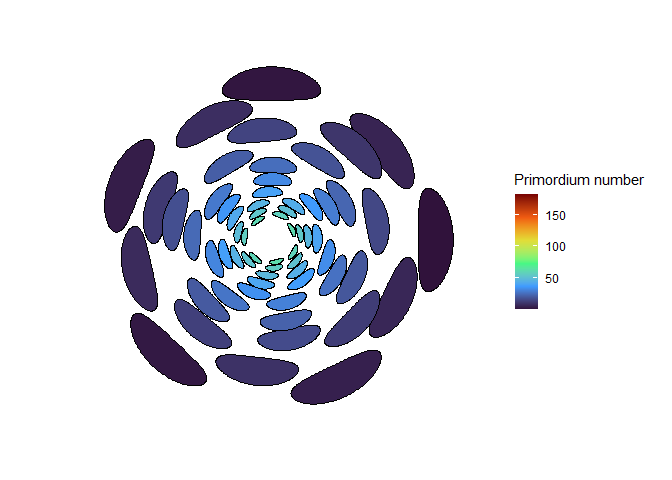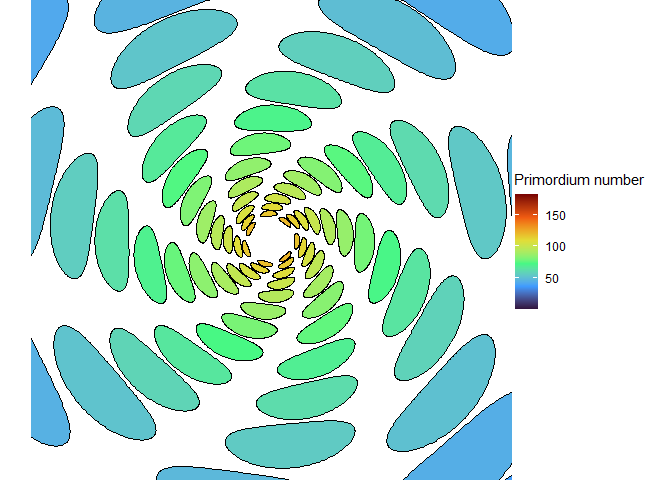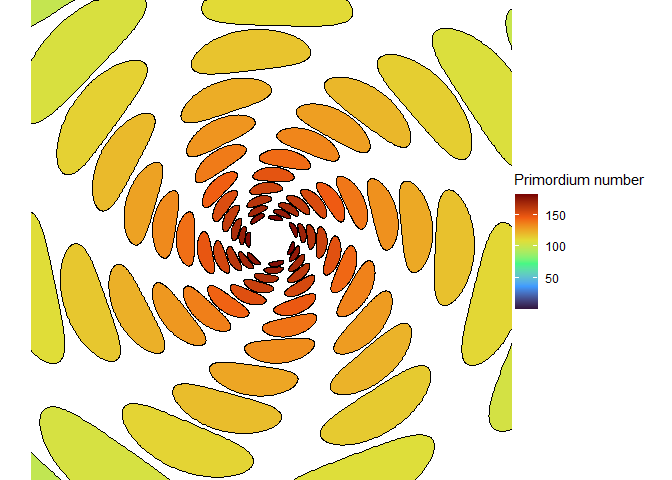
This blew my mind for two reasons. First, despite neither the Fibonacci sequence nor the golden ratio being in the code, the system settled out into a pattern of primordia emerging the golden angle to each other, forming contact parastichies in adjacent numbers in the Fibonacci series. Second, the system starts out with bilateral symmetry but somehow loses it. I would think that the lowest point of energy would be completely opposite the first primordium, then exactly in between two primordia, forming a decussate pattern, but that isn’t what happens. So, I dug further into simulation to try to understand the moment that symmetry is lost.
The meristem in this simulation starts with one primordium, and then another is immediately added 180° opposite to it. But then once these first two move away a little, instead of adding primordia in both positions 90° to the first two, only one of those positions is recognized as the minimum energy and used for initiating a primordium. That third primordium moves away a little bit before the fourth can be added. Something similar happens with the next two primordia, and now the symmetry is lost, and the pattern devolves into a spiral.
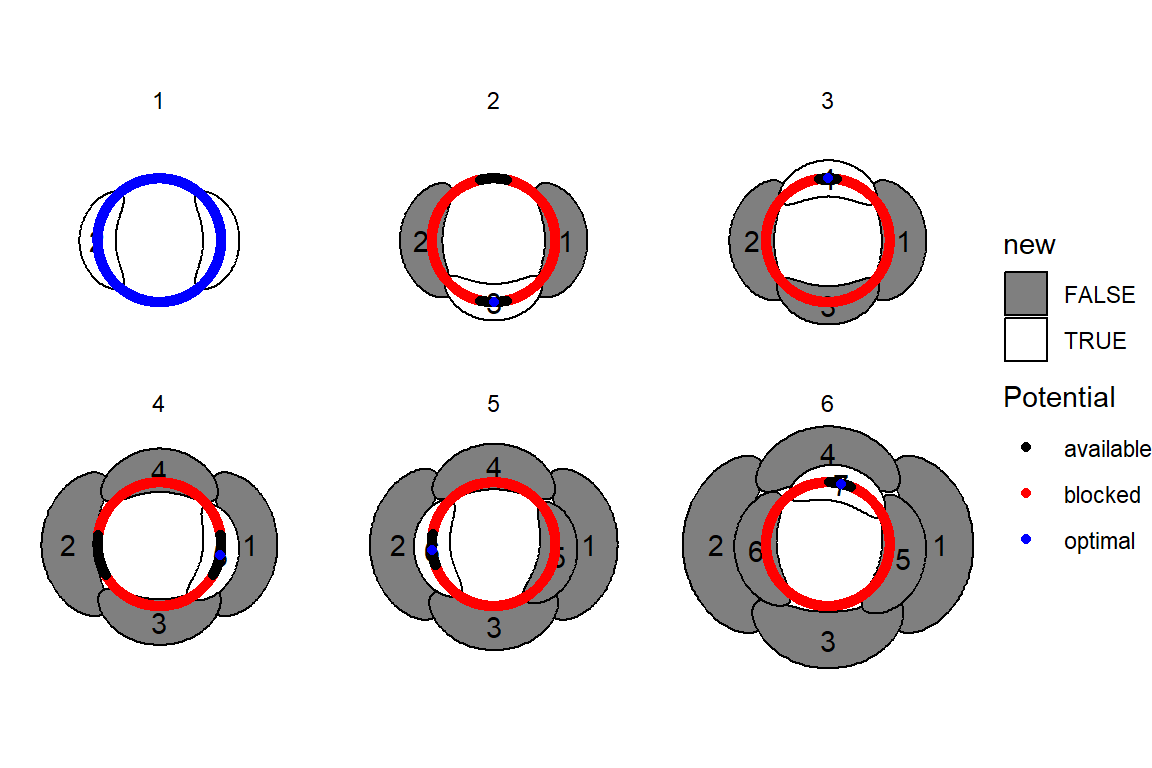
Now we are totally out of the realm of biology and into the realm of computer science. Any computer processor has limits to how precisely it can store a number. It is very common to see a rounding error of about \(10^{-16}\) in floating point math. And that was the difference in inhibition energy between those two points completely opposite each other in step 2. I told the computer to only use the minimum, and it did. So I modified my code to use R’s all.equal function, so that it would put primordia at all points equal to the minimum energy, for the human definition of equal rather than the computer definition of equal. And here’s what I got:
Still image
So let’s modify George Cox’s quote to say, “all models are wrong, but some are useful when simulated incorrectly”! I checked across a range of inhibitory sphere sizes. Above a certain size, I always get a distichous pattern. Below that, if I start with a symmetrical system and use all.equal, I always get symmetrical decussate or whorled patterns. If, below the distichous threshold, I start with an asymmetrical system and/or let floating point math do its thing, I always get a spiral (or in one case a weird quasi-decussate pattern). Douady and Couder (1996c) also found distichous patterns when the sphere of inibition was large, and a mix of spiral and decussate patterns below that, although they never mention computer rounding errors. However, they put much, much more effort into their research than I am willing to put into this blog post, so I will give them the benefit of the doubt that they had it figured out.
Let’s have a couple more animations for the road. Here’s a distichous pattern that arises despite being initialized in an asymmetrical system.
Still image
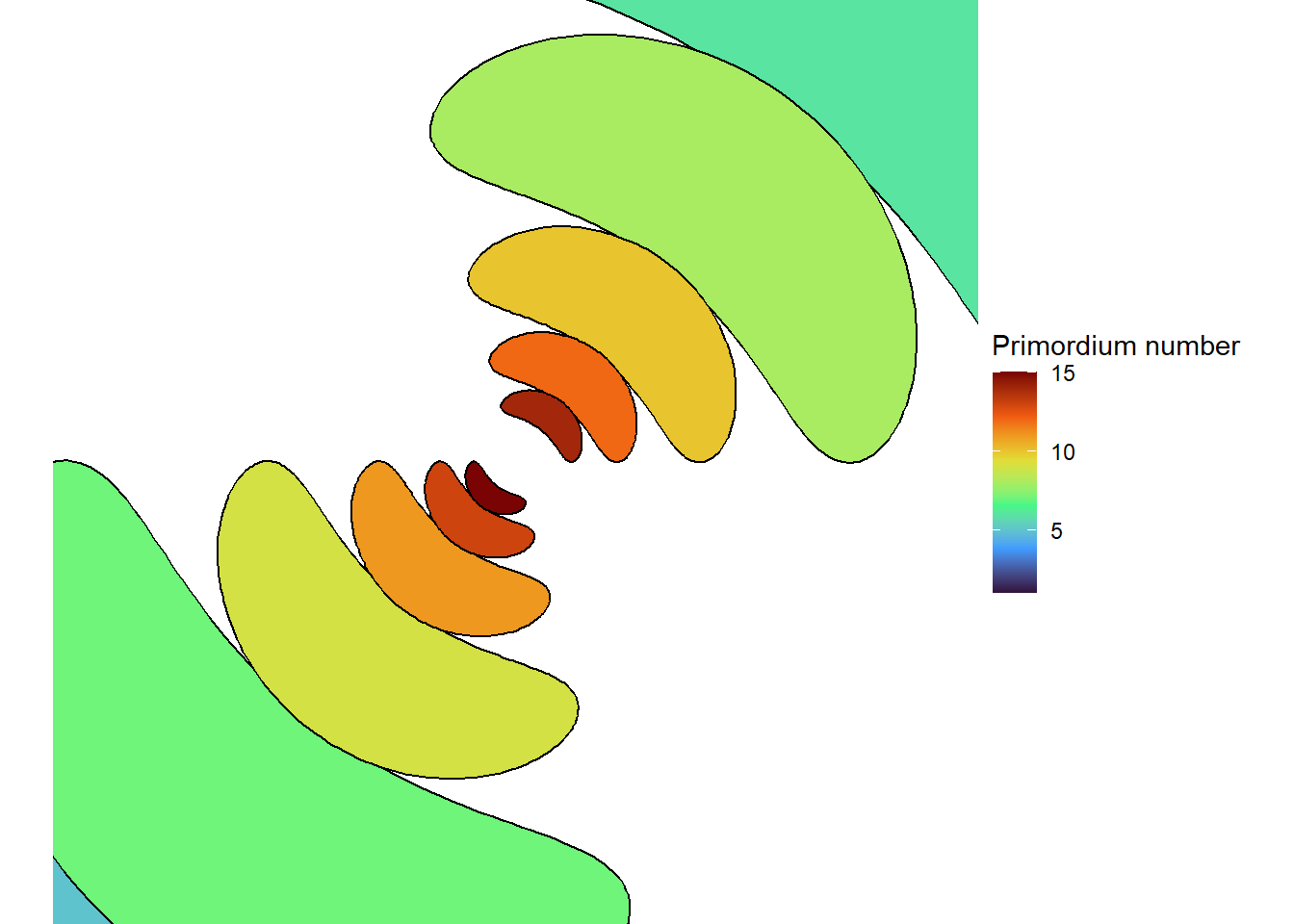
With the right size, we can get seven spirals, a Lucas number! (Vi Hart discusses these in her third video.)
Still image
At the molecular level
So the TL;DR version of Douady and Couder is, leaves and flowers can form amazing spiral patterns just by trying to stay out of each other’s way, because living things are never perfectly symmetrical. And some people have figured out why Fibonacci and Lucas numbers and their associated angles show up (Bravais and Bravais 1837; Okabe 2015), but even as good at math as I am I think I’m content to let it be a beautiful mystery to me. But as a biologist, I would remiss if I didn’t talk about the mechanisms by which the primordia repel each other.
I found a couple good scientific reviews that discuss the genes and hormonal action in the meristem with regards to phyllotaxis (Barton 2010; Shi and Vernoux 2019). Based on the inhibitory field hypothesis supported by Douady and Couder’s simulations, I would expect that some molecule is produced at the center of each primordium, passively diffuses outward, and inhibits the formation of new primordia wherever its concentration is high enough. However, the opposite seems to be true, in that there is a hormone that causes primordia to form, not a hormone that prevents them from forming. If the plant hormone auxin is applied to a point on the apex periphery of a meristem, a primordium will form at that point. Auxin applied to the apex (AKA central zone) does not cause primordia to form, probably because the hormone cytokinin is present in the apex and is generally known to block the action of auxin (both of these hormones play many roles within plants).
The cool thing about auxin is that it doesn’t just passively diffuse through the plant, but is actively transported from cell to cell in particular directions. Important to the formation of primordia is the protein PIN1, which sits in the cell membrane and transports auxin across to the adjacent cell. It is named because PIN1 mutants can’t form flowers, and therefore have an inflorescence shaped like a pin. PIN1 is most commonly expressed on just one side of a cell, so the auxin is pumped on one direction. In most of the meristem, PIN1 protein tends to congregate where the auxin levels are highest, causing a positive feedback loop that will concentrate all the auxin into one place, where the new primordium forms. However, once the new primordium starts protruding outward, a crease forms between the new primordium and the meristem, and PIN1 switches sides, pushing auxin away from that crease. Thus, auxin bounces around and around the meristem, finding an empty spot and then leaving it once the primordium begins to form.
So the “inhibitory field” hypothesis used by Douady and Couder and many before them is correct but only for a pretty abstract definition of inhibitory field, in that the “field” is a pattern of proteins placed on cell membranes such that they move a hormone in a certain direction. (Maybe that’s not abstract at all to a physicist. I don’t know.) Vi Hart’s description of primordia moving around to gobble up hormone is not quite right, although her videos are otherwise fantastic (aside from not knowing what a magnolia fruit was, but that’s forgivable). And I am sure my explanation of auxin transport is also a gross oversimplification (for example there are important auxin transporters besides PIN1, some aspects of the system still aren’t fully understood, and mechanical stress on the cells is probably involved), but hopefully it gets us all a bit closer to understanding the truth of what is happening. Wrong but useful models!
About those lycopods
Getting back to the study on lycopod fossils (Turner et al. 2023), the presence of non-Fibonacci numbers of contact parastichies (often \(n\) and \(n + 1\)) in some modern and many ancient lycopod species must mean that the meristem is a different shape or uses a different molecular mechanism of organizing itself as compared to most plants. They noted that species with non-Fibonacci phyllotaxis also tend to have dichotomous branching, which means that instead of a branch developing from an axillary bud, the meristem itself can split right down the middle into two (Gola 2014). Lycopods are very distantly related to other vascular plants, so it makes sense that they might do things differently. If you ever see a club moss and get a “not like other plants” vibe, now you know why.
For one last sacred geometry before we go, here are some animations of the direction auxin would move back and forth across the meristem, forming a star that never closes. Likewise, may your growth never be complete!
Still image
Still image
References
Azpeitia, Eugenio, Gabrielle Tichtinsky, Marie Le Masson, Antonio Serrano-Mislata, Jérémy Lucas, Veronica Gregis, Carlos Gimenez, et al. 2021. “Cauliflower Fractal Forms Arise from Perturbations of Floral Gene Networks.” Science 373 (6551): 192–97. https://doi.org/10.1126/science.abg5999.
Barton, M. K. 2010. “Twenty Years on: The Inner Workings of the Shoot Apical Meristem, a Developmental Dynamo.” Developmental Biology 341: 95–113. https://doi.org/10.1016/j.ydbio.2009.11.029.
Bravais, L., and A. Bravais. 1837. “Essai Sur La Disposition Des Feuilles Curvisériées.” Annales Des Sciences Naturelles, 2nd series, 7: 42–110.
Douady, S., and Y. Couder. 1996a. “Phyllotaxis as a Dynamical Self Organizing Process Part I: The Spiral Modes Resulting from Time-Periodic Iterations.” Journal of Theoretical Biology 178 (3): 255–74. https://doi.org/10.1006/jtbi.1996.0024.
———. 1996b. “Phyllotaxis as a Dynamical Self Organizing Process Part II: The Spontaneous Formation of a Periodicity and the Coexistence of Spiral and Whorled Patterns.” Journal of Theoretical Biology 178 (3): 275–94. https://doi.org/10.1006/jtbi.1996.0025.
———. 1996c. “Phyllotaxis as a Dynamical Self Organizing Process Part III: The Simulation of the Transient Regimes of Ontogeny.” Journal of Theoretical Biology 178 (3): 295–312. https://doi.org/10.1006/jtbi.1996.0026.
Gola, Edyta M. 2014. “Dichotomous Branching: The Plant Form and Integrity Upon the Apical Meristem Bifurcation.” Frontiers in Plant Science 5. https://doi.org/10.3389/fpls.2014.00263.
Newell, Alan C., and Patrick D. Shipman. 2005. “Plants and Fibonacci.” Journal of Statistical Physics 121 (5/6): 937–68. https://doi.org/10.1007/s10955-005-8665-7.
Okabe, Tayuka. 2015. “Biophysical Optimality of the Golden Angle in Phyllotaxis.” Scientific Reports 5: 15358. https://doi.org/10.1038/srep15358.
Shi, Bihai, and Teva Vernoux. 2019. “Patterning at the Shoot Apical Meristem and Phyllotaxis.” In Plant Development and Evolution, edited by Ueli Grossniklaus, 131:81–107. Current Topics in Developmental Biology. Elsevier. https://doi.org/10.1016/bs.ctdb.2018.10.003.
Swinton, Jonathan, Erinma Ochu, and The MSI Turing’s Sunflower Consortium. 2016. “Novel Fibonacci and Non-Fibonacci Structure in the Sunflower: Results of a Citizen Science Experiment.” Royal Society Open Science 3 (5). https://doi.org/10.1098/rsos.160091.
Turner, Holly-Anne, Matthew Humpage, Hans Kerp, and Alexander J. Hetherington. 2023. “Leaves and Sporangia Developed in Rare Non-Fibonacci Spirals in Early Leafy Plants.” Science 380 (6650): 1188–92. https://doi.org/10.1126/science.adg4014.
Reuse
CC-BY